Project 2 - Fun with Filters and Frequencies!
Part 1.1: Finite Difference Operator
We compute the derivative in the x and y directions, and then combine them via the Pythagorean theorem to obtain gradient magnitude.
def edge_image(gradient_x, gradient_y):
return np.hypot(gradient_x, gradient_y)

Initial image of a camera man
|
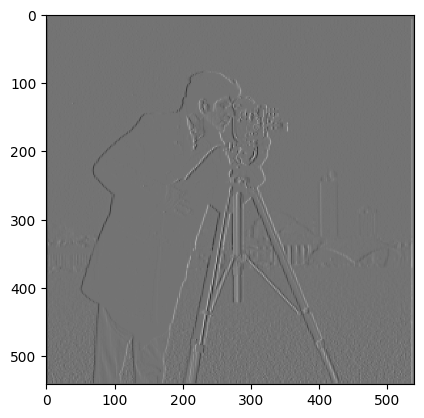
Derivative in the x direction. This comes from kernel [[1, -1]], which takes a local pixel difference. Notice how the tripod is very clearly defined, where things like the outline of the cameraman's jacket isn't.
|
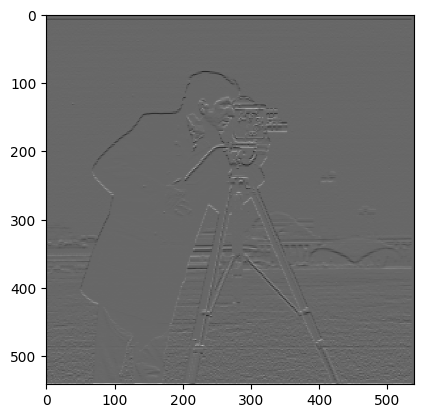
Derivative in the x direction. This comes from kernel [[1], [-1]], which takes a local pixel difference across the y channel (note the bracketing). Here, notice the bare minimum definition of the tripod. Look at the opera house in the background, and how the curves are very clearly defined.
|
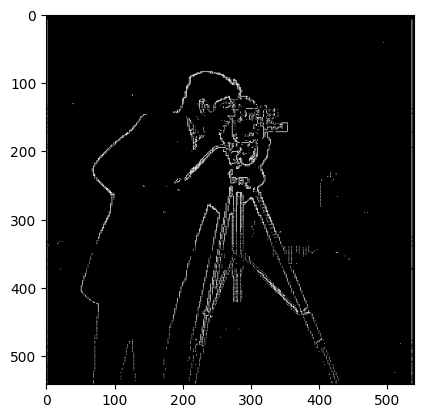
Binarized output after taking the output to compute gradient magnitude. In order to perform binarization, we took all pixel values in top 97.5% percentile, resulting in the figure. There are other options that are more standard (thresholding by a high value, say 95%), but we believe that this method would provide more consistent results across images.
|
Part 1.2: Derivative of Gaussian Filter

Blurred output. The gaussian kernel was constructed using an outer product of a 1D gaussian sample.
|

Derivative in the x direction. Note the darkness and less defined features within the tripod in comparison to the image above.
|

Derivative in the x direction. Reflects the comments for the x-direction derivative image (on the left), the opera is now barely visible.
|
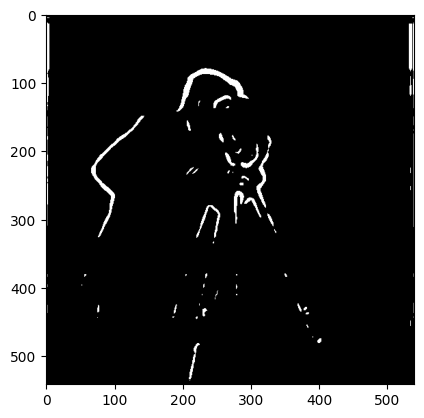
Binarized output after taking the hypotenuse to compute gradient magnitude. In order to perform binarization, we took all pixel values in top 97.5% percentile, resulting in the figure.
|
Notable Differences:
Clearly, there edges being captured less accurately post binarization. Additionally, areas that were close to portions of the image with minimal change (which would be erased by a derivative) have finally met their maker - the blur forces all edges to be lower in value, making the top percentage a more elite category.
One "magic" filter for blurring and convolution?
Our derivative filter is pretty primative. So we tried to convolve the larger gaussian kernel itself to see if it would compose the convolution.
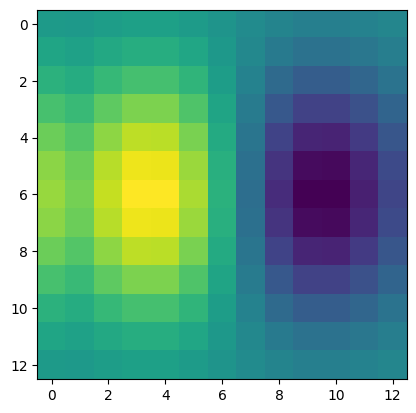
Derivative in the x direction. This comes from kernel [[1, -1]] on a gaussian kernel with size 13 and stdev 3, which takes a local pixel difference.
|
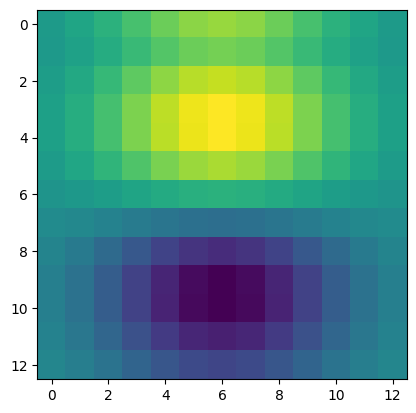
Derivative in the x direction. This comes from kernel [[1, -1]] on a gaussian kernel with size 13 and stdev 3, which takes a local pixel difference.
|

Lo and behold, the same image, twice!
|
Part 2.1: Image Sharpening
Listed below are some examples of sharpening done using the 'alpha sharpening technique', which consisted of adding alpha * [high pass results] to the original image.

Original image of the Taj Mahal.
|
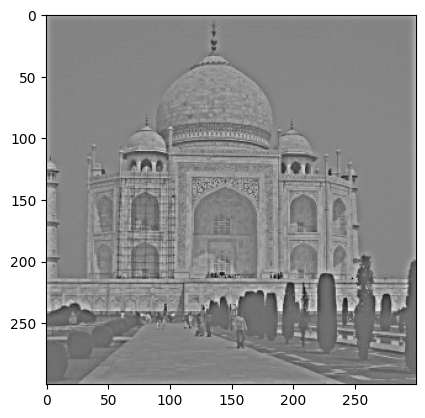
Sharpened with alpha = 5
|
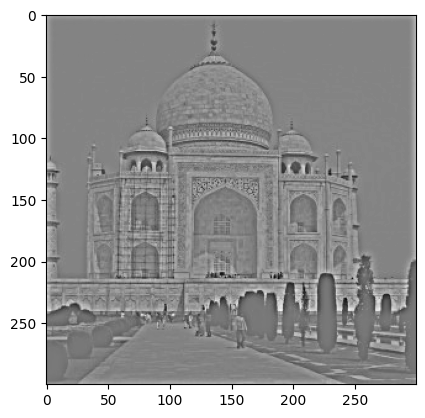
Sharpened with alpha = 10
|
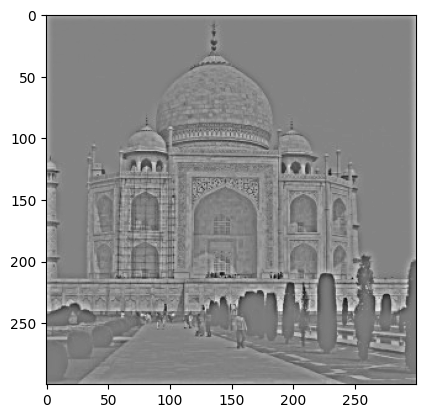
Sharpened with alpha = 15
|
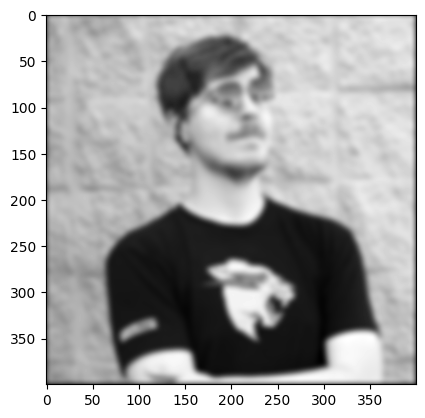
Blurred image of GOAT Mr. Beast, kernel size 13 and stdev 3.
|

Sharpened with alpha = 5
|

Sharpened with alpha = 10
|

Sharpened with alpha = 15
|
Observations
While the image isn't too similar to the original, the effects of sharpening are somewhat clear. We can clearly see defined edges around Jimmy's (MrBeast) shirt, and the MrBeast YouTube logo is very clearly standing out from the rest of the black tshirt.
Part 2.2: Hybrid Images
Sample Output

Base image of Nutmeg the cat.
|

Base image of Derek.
|
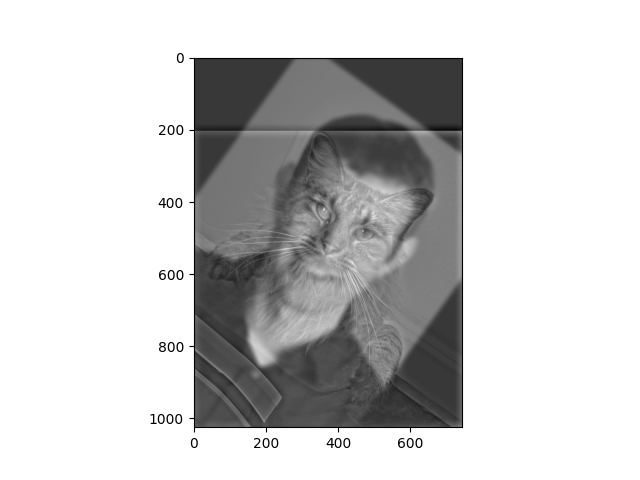
Hybrid Image.
|
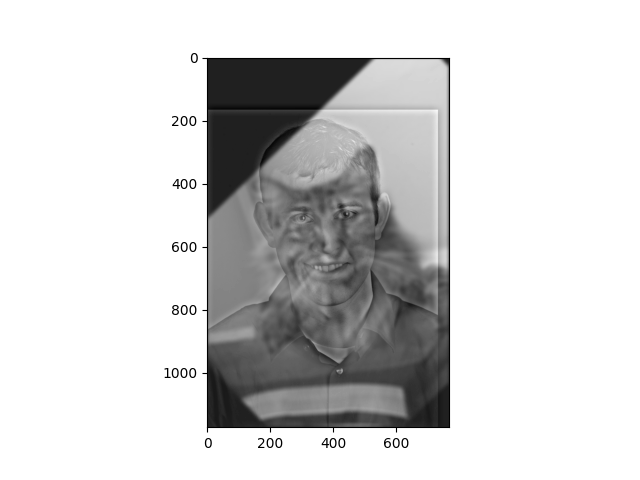
Hybrid Image, with the low and high frequencies switched.
|
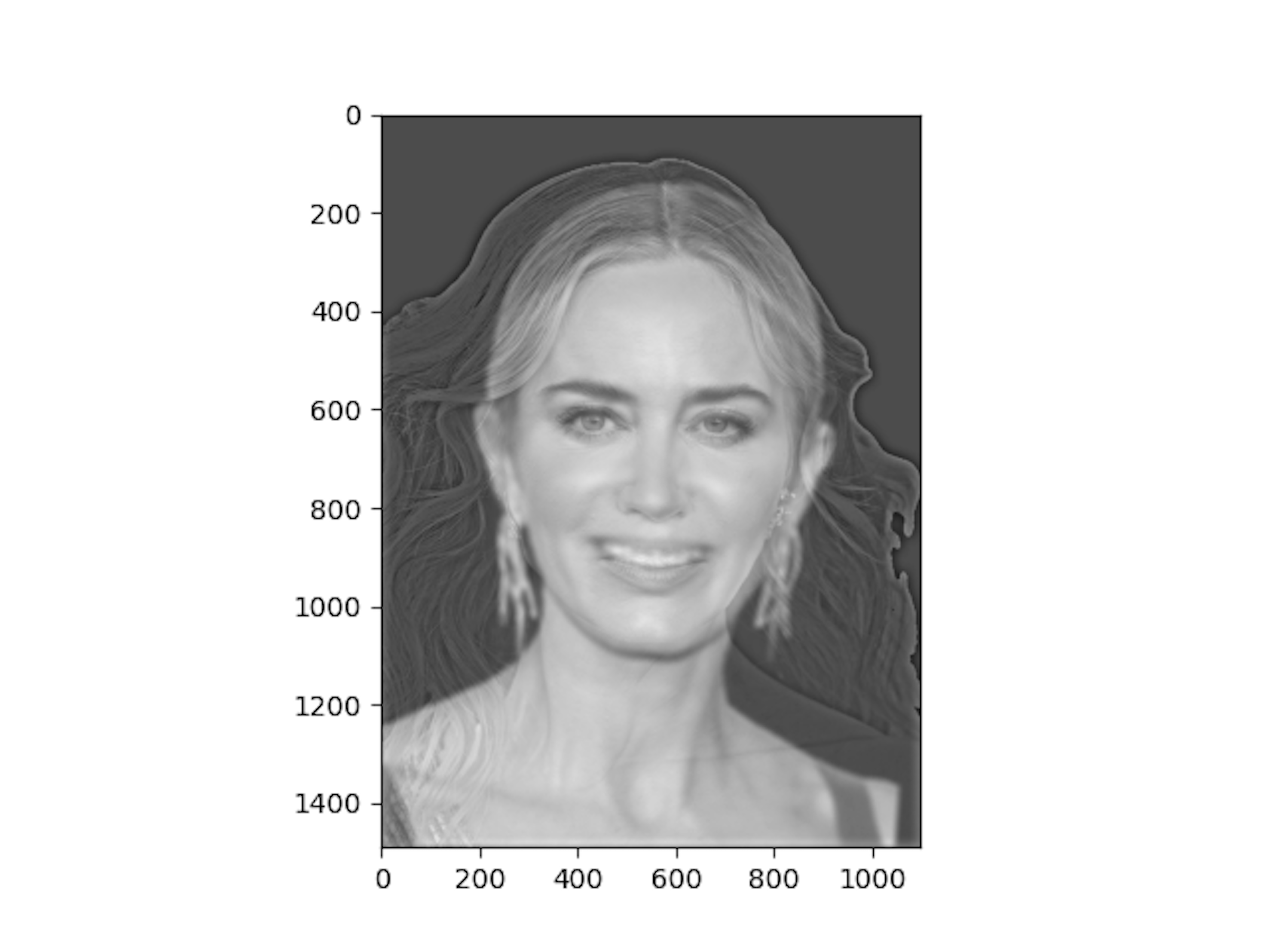
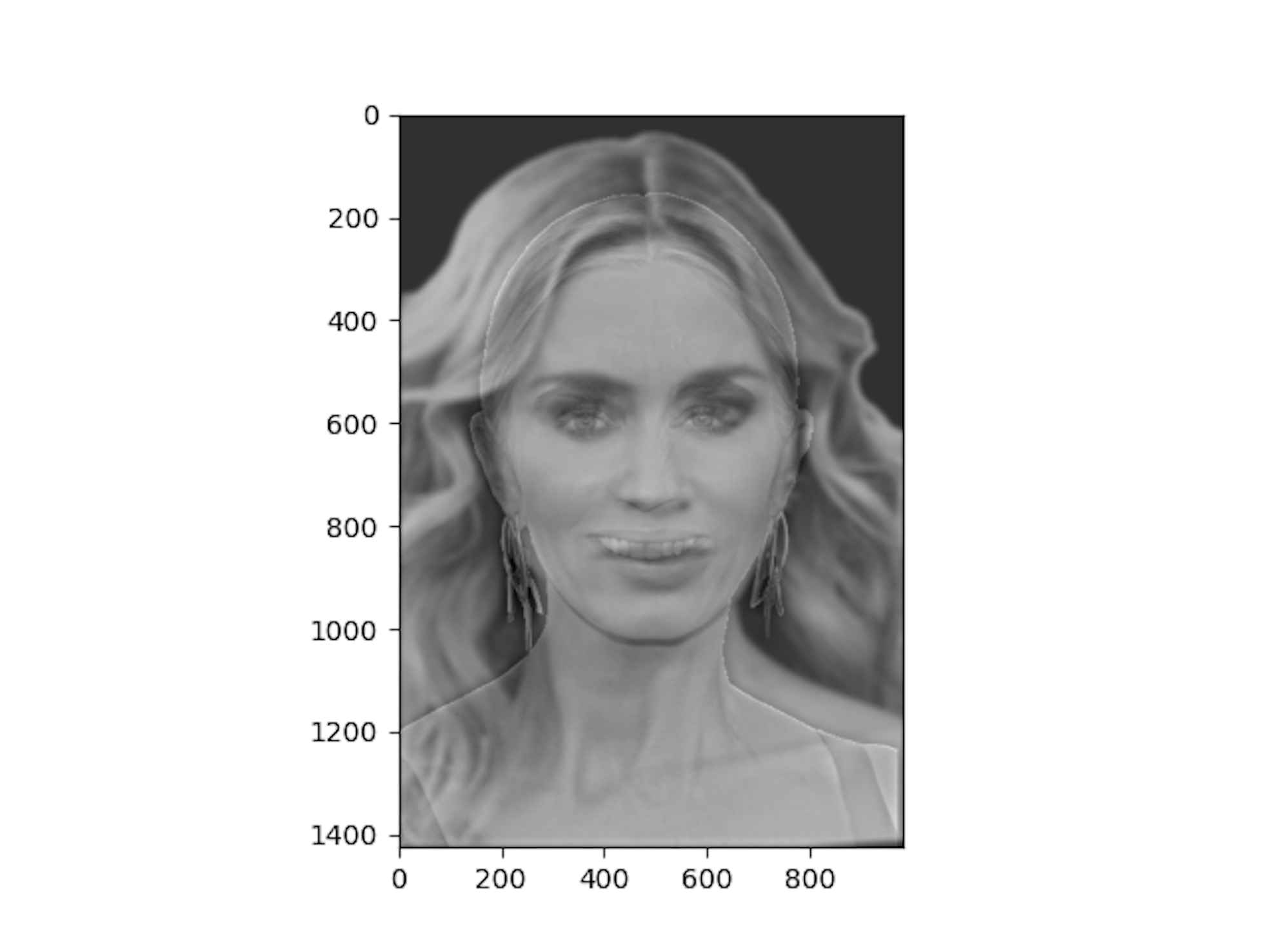
Change of Expression - Emily Blunt
I am convinced that one of the best actresses is Emily Blunt! To commemorate our favorite actress in god-knows-how-many-movies-I've watched, I tried to capture her in two emotions - one smiling with teeth, and one without. Not quite a Mona Lisa, but it does give off some of those vibes that we discussed Da Vinci
trying to instill.
Morph between different objects - Ed Sheeran and a Wolf
This was an example I originally saw someone doing a similar exercise in the past perform. To benchmark whether I was on the right track (getting similar results to "state of the art"), I listed the output. Here is the link to the original report, and the example: https://ddavidhahn.github.io/194-26_Project3/
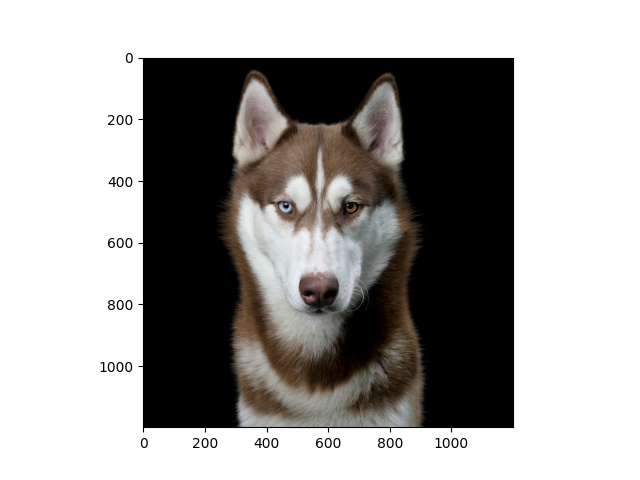
Base image of a brown dog.
|

Image of Ed Sheeran.
|

Hybrid, with Ed Sheeran being the high frequencies.
|
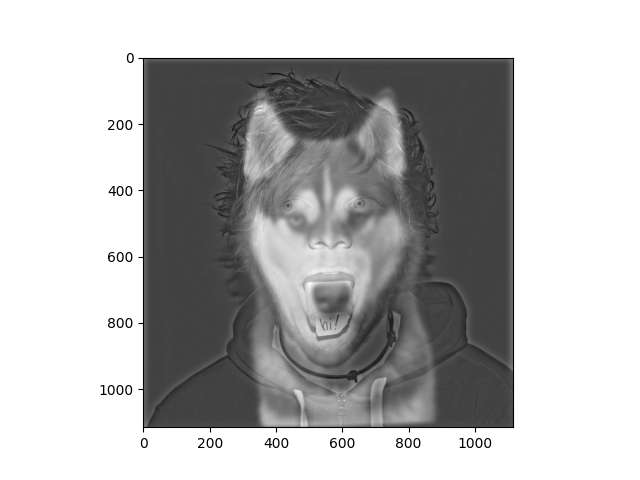
Hybrid with the dog being the higher frequency.
|
Part 2.3: Gaussian and Laplacian Stacks
The journey towards the Oraple
As you can see the images on the left reprsent lower frequencies, the ones in the center being more middle, and the last being the highest. There is no clear visible split between the apple and the orange thanks to the Gaussian pyramids for the masks (from the paper, second algorithm), alongside a smoothing region
Part 2.4: Multiresolution Blending
Just a bunch of fun down here

PewDiePie, the original YouTuber
|

Mr Beast, the current reigning king of YouTube and of my childhood :)
|

The greatest YouTubers of all time, prove me wrong! Made with a similar, vertical mask
|
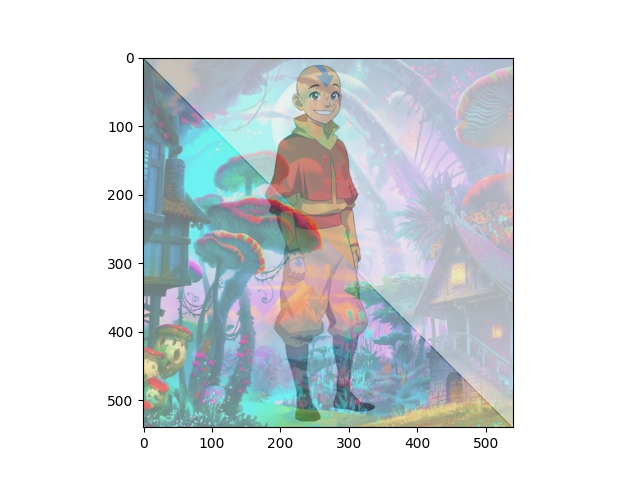
Aang on shrooms. Made with an upper triangular mask, with a lower than default initial value for the region where the ones are supposed to be. Cool thing was that the Aang image was transparent.
|
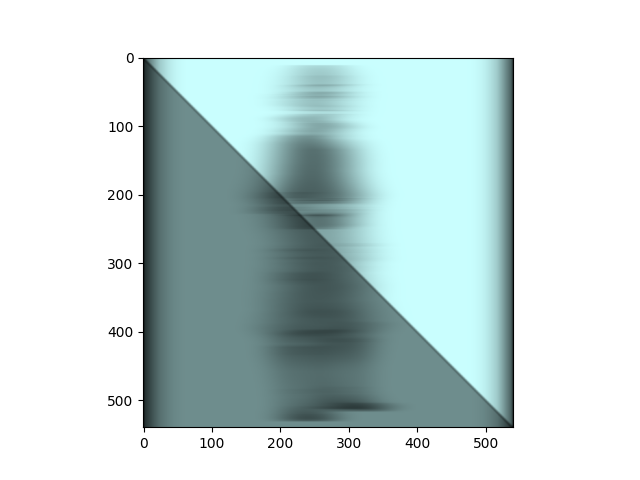
The mask with Aaang
|
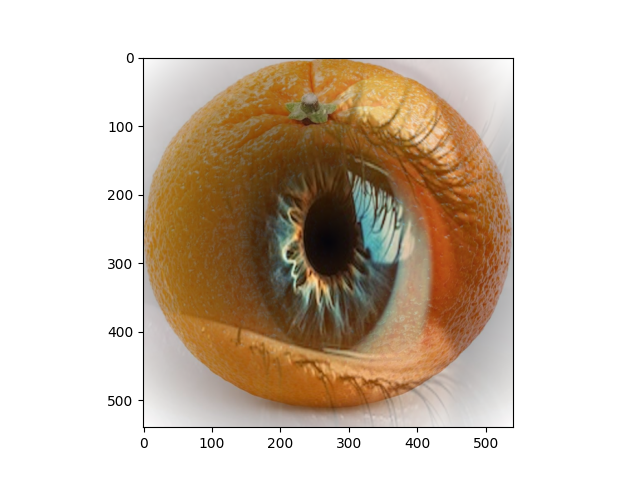
If the other two seem a litte ... weird, what about this one? Check out an eyeball inside an orange!
|
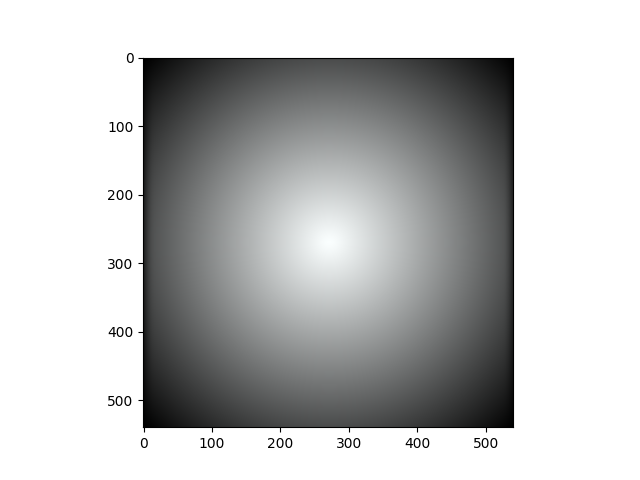
The mask
|

The eye
|

The orange
|